
Generally, it involves moving the constant to the other side of the equation and finding a constant that allows us to write the right hand side of the equation in a form resembling vertex form, applying that constant to the left side of the equation, then shifting the constant on the left side back to the right side. Refer to the completing the square for a detailed explanation. Let’s double check our -coordinate by using the standard method (plugging. y a ( x 2 + b a x + b 2 4 a 2) b 2 4 a + c. Putting f into vertex form, we have: y a x 2 + b x + c. is a vertical parabola with axis of symmetry parallel to the y axis and has a vertex V with coordinates (h, k), x - intercepts when they exist and a y - intercept as shown below in the graph. Then, you create a new quadratic function by multiplying by a factor of : g ( x) f ( x) a x 2 + b x + c. How Do You Find the Vertex of a Quadratic Function The vertex of a quadratic equation is the minimum or maximum point of the equation. Review Vertex and Intercepts of a Quadratic Functions The graph of a quadratic function of the form.
Solution: The quadratic formula for this function is. Let's say you have a quadratic function f ( x) a x 2 + b x + c. Converting from standard form to vertex formĬonverting a quadratic equation from standard form to vertex form involves a technique called completing the square. Use the quadratic formula to identify the entire vertex of the function, and then verify the answer using the standard method. This is due to the nature of positive/negative numbers. However, if, like in equation (2.), the signs are different from those in the general vertex form equation, we need to take the signs into account for h, the sign of the x-coordinate of the vertex is opposite of that in the vertex form equation for k, the sign of the y-coordinate is the same as that in the vertex form equation. If, like in equation (1.) above, the signs in the equation match that of the generalized vertex form, then we can read off (h, k) as the vertex. We need to remember the vertex form a(x - h) 2 + k. The above examples show that we can't just read off the values based on their position in the equation.

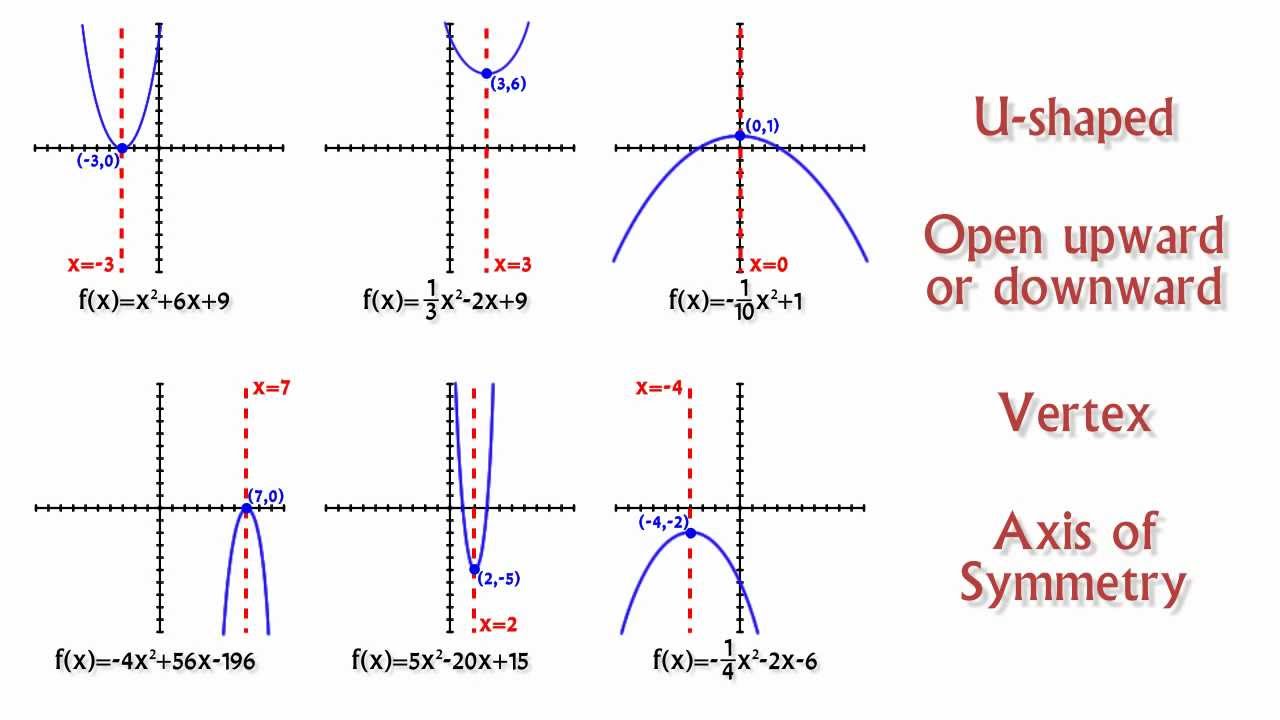
The following are two examples of quadratic equations written in vertex form: Vertex form can be useful for solving quadratic equations, graphing quadratic functions, and more. This is something that we cannot immediately read from the standard form of a quadratic equation. Where a is a constant that tells us whether the parabola opens upwards or downwards, and (h, k) is the location of the vertex of the parabola. The vertex form of a quadratic equation is The standard form of a quadratic equation is ax 2 + bx + c. Vertex form is another form of a quadratic equation. The following video looks at the various formats in which Quadratic Functions may be written as.Home / algebra / solving equations / vertex form Vertex form If a is positive then it is a minimum vertex. The vertex form is useful because we can see the turning point or vertex of the graph.įor example, the turning point or vertex of y = a( x − h) 2 + k Y = a( x − h) 2 + k where a, h and k are real numbers Vertex of quadratic function is the highest point present on the graph if direction of opening is downwards for the given quadratic function. The vertex form of a quadratic equation is What is the vertex of such a quadratic function Vertex of the quadratic function is the lowest point present on the graph if direction of opening is upwards. The factored form is useful because we can see the x-intercepts (which are also the roots when the function is zero).įor example, the x-intercepts of y = a( x + b)( x + c) are (− b, 0) and (− c, 0) Y = a( x + b)( x + c) where a, b and c are real numbers and a is not equal to zero. The factored form of a quadratic equation is Y = ax 2 + bx + c where a, b and c are real numbers and a is not equal to zero. And how is the general formula for the vertex point f(x)1a(x2+b/, ( Factor out ) f(x)1a(x2+b/, ( Complete the square ) f(x)1a((x+b/(, ( Use the. The general form of a quadratic equation is We can write quadratic functions in different ways or forms: The vertex form of a quadratic function is an expression that easily provides the coordinates of the vertex point on the parabola. Scroll down the page for more examples and solutions for quadratic equations.
VERTEX OF QUADRATIC FUNCTION HOW TO
The following diagram shows how to use the vertex formula to convert a quadratic function from general form to vertex form.


 0 kommentar(er)
0 kommentar(er)
